Bayesian Learning for High Order Data

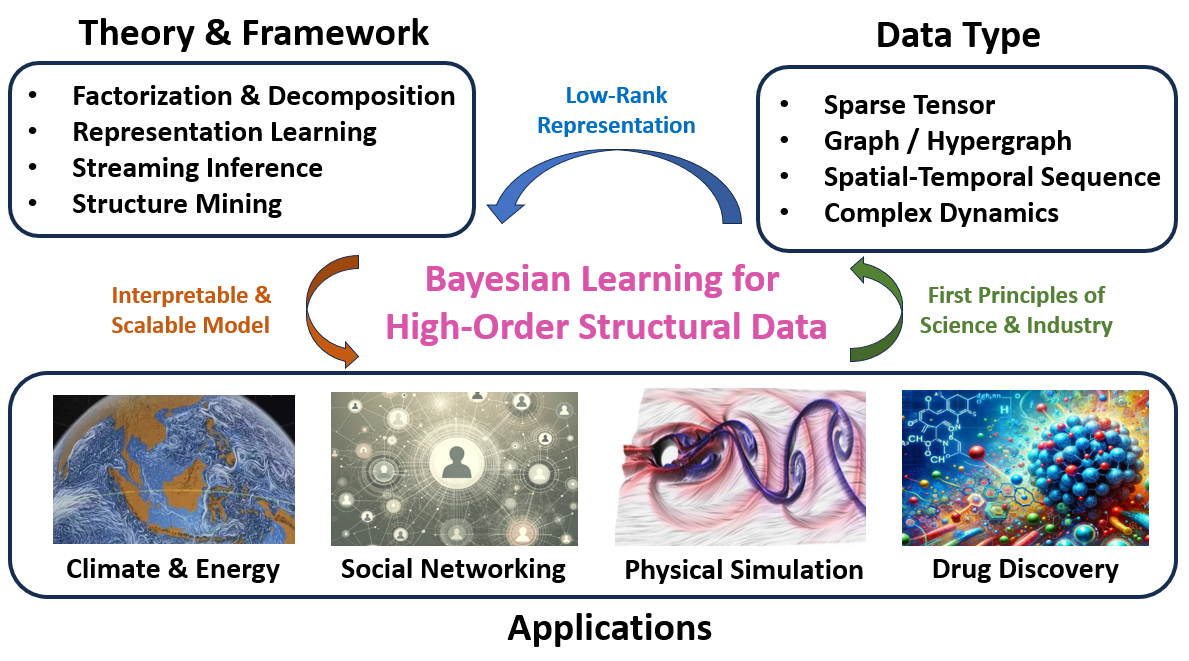
Overview

Bayesian learning provides a principled framework for uncertainty quantification and model selection in high-dimensional data analysis. This research direction focuses on developing scalable Bayesian methods for tensor data and high-order interactions.

Key Research Areas

1. Tensor Decomposition with Bayesian Priors

• Objective: Develop Bayesian tensor decomposition methods that incorporate domain knowledge through structured priors
• Challenges: Scalability for large-scale tensors, choice of appropriate priors
• Applications: Recommender systems, neuroimaging data analysis, social network analysis

2. Uncertainty Quantification in Tensor Models

• Objective: Provide reliable uncertainty estimates for tensor-based predictions
• Methods: Variational inference, Markov Chain Monte Carlo (MCMC)
• Benefits: Robust decision making, model interpretability

3. Scalable Bayesian Inference

• Objective: Develop efficient inference algorithms for large-scale tensor data
• Techniques: Stochastic variational inference, distributed computing
• Impact: Enables Bayesian analysis of real-world large datasets

Research Roadmap

Phase 1: Foundation (Months 1-6)

• Literature review of existing Bayesian tensor methods
• Development of basic Bayesian tensor decomposition framework
• Implementation of baseline methods

Phase 2: Innovation (Months 7-12)

• Design of novel prior structures for tensor data
• Development of efficient inference algorithms
• Theoretical analysis of convergence properties

Phase 3: Application (Months 13-18)

• Application to real-world datasets
• Performance evaluation and comparison
• Publication of results

Technical Approach

Our approach combines:

• Probabilistic modeling: Bayesian framework for uncertainty quantification
• Tensor algebra: Efficient computation with tensor operations
• Variational inference: Scalable approximation methods
• Domain-specific priors: Incorporation of expert knowledge

Expected Outcomes

1. Novel algorithms: Scalable Bayesian tensor decomposition methods
2. Software package: Open-source implementation
3. Theoretical contributions: Convergence analysis and error bounds
4. Applications: Real-world case studies demonstrating effectiveness

Related Work

• Bayesian CP decomposition
• Probabilistic tensor factorization
• Variational inference for tensors
• Uncertainty quantification in deep learning

This research direction aims to bridge the gap between theoretical Bayesian methods and practical applications in high-dimensional data analysis.