中文版 / Chinese Version

Tensor Learning for Real-World Structural Data

Overview

In real-world physical and engineering systems, data often exhibits high-order (multi-way) structure and an intrinsic low-rank nature. Examples include spatiotemporal measurements, dynamical systems, and complex networks, all of which are naturally represented as tensors. Achieving compact and interpretable representations for such high-order structural data is a core challenge at the intersection of modern AI and scientific computing.

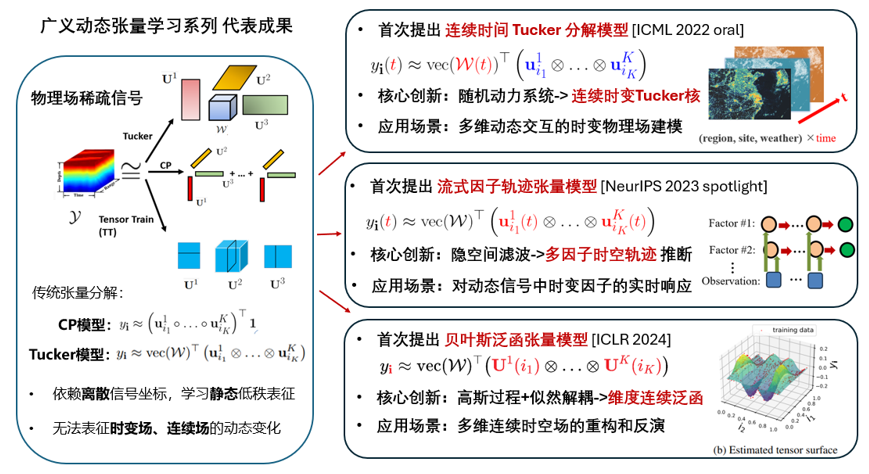
Motivation & Challenges

• High-Order Structure: Real-world data is rarely simple tabular or sequential data; instead, it is often multi-modal and multi-dimensional (e.g., time, space, frequency, entity-relation).
• Low-Rank Essence: Despite high dimensionality, the underlying structure can often be well-approximated by low-rank models (e.g., principal components, low-rank decompositions, low-rank perturbations).
• Need for Compact Representations: Structural data in the physical world demands compact and efficient representations for downstream modeling, reasoning, and generation.
• Large Model Adaptation & MOE Systems: Modern paradigms such as LoRA (Low-Rank Adaptation) and Mixture of Experts (MOE) leverage low-rank ideas for efficient parameter updates and expert routing, highlighting the universality of low-rank principles.
• Generative AI for Structure: Incorporating high-order structure and low-rank constraints into generative models (e.g., diffusion models, VAEs, GANs) is key to improving generation quality and physical consistency.

Key Research Directions

1. Low-Rank Decomposition and Dynamic Modeling of High-Order Tensors

• Goal: Develop low-rank tensor decomposition methods for complex scenarios such as streaming, dynamic, and continuously indexed data.
• Challenges: Address streaming data, dynamic evolution, irregular observations, noise, and interpretability in real-world settings.
• Approach: Combine Bayesian inference, neural networks, and physical priors for adaptive modeling of dynamic tensors.

2. Generative Modeling for Structural Data

• Goal: Integrate high-order structure and low-rank constraints into generative models, enabling unified modeling of tensors, hypergraphs, and complex dynamics.
• Approach: Perform low-rank modeling in the latent space, leveraging diffusion processes, variational inference, and other generative techniques.
• Applications: Molecular structure generation, trajectory prediction, complex network modeling, and more.

3. Low-Rank Principles in Large Model Adaptation and MOE Systems

• Goal: Harness low-rank ideas to improve parameter efficiency and generalization in large models.
• Approach: Use LoRA for low-rank gradient projection, low-rank decomposition in expert routing, and parameter-efficient fine-tuning.
• Significance: Enable efficient adaptation of large models to diverse tasks and domains.

4. Compact Representation for Physical Structural Data

• Goal: Fuse physical priors with AI methods to achieve compact and interpretable representations for complex real-world structural data.
• Approach: Generalized low-rank dynamic representations, first-principle-embedded AI models, and multi-modal fusion (frequency, dynamics, physical experiments).

Roadmap

Phase 1: Theory & Method Development (Months 1-6)

• Review theoretical foundations of high-order tensor decomposition and low-rank modeling
• Develop algorithms for dynamic/streaming/sparse tensor decomposition
• Prototype modules for structure-aware generative AI

Phase 2: Multi-Modal Fusion & Physical Priors (Months 7-12)

• Integrate physical priors and neural networks for improved interpretability and generalization
• Validate low-rank principles in LoRA, MOE, and large model adaptation
• Advance generative models for structural data

Phase 3: Real-World Applications & System Integration (Months 13-18)

• Deploy in real-world scenarios: molecular dynamics, environmental monitoring, complex networks
• Develop open-source toolkits for the community
• Publish high-impact papers and drive the research frontier

Technical Innovations

• Bayesian Low-Rank Tensor Decomposition: Efficient modeling of dynamic tensors via Bayesian inference and low-rank decomposition
• Structure-Constrained Generative AI: Incorporating high-order structure and low-rank priors into generative models
• Parameter-Efficient Large Model Adaptation: Low-rank updates in LoRA, MOE, and related paradigms
• Physics-AI Fusion: Embedding first-principle knowledge and frequency/dynamics analysis for interpretable models

Related Images

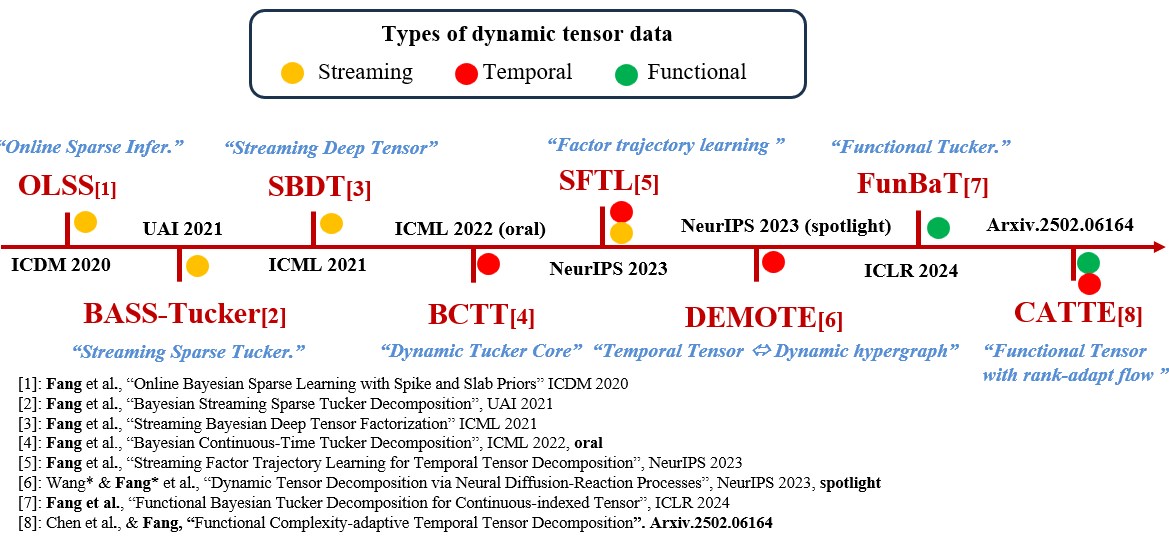
Expected Outcomes

1. Theoretical Advances: New theory for Bayesian low-rank modeling of high-order tensors
2. Algorithmic Tools: Efficient algorithms for dynamic, streaming, and sparse tensor decomposition and generative modeling
3. Open-Source Platform: Generative AI toolkit for structural data
4. Real-World Impact: Applications in molecular dynamics, environmental science, complex networks, and beyond

This research direction aims to advance compact representation and generative modeling for high-order structural data, bridging AI and the physical world.